2012-11-18

Eclipseでgitを使う（ブランチ編）

git eclipse

前回はEclipseでgitを使う導入まで説明したので、今回はブランチの使い方について説明します。
といっても、全く難しいことはありません。
~~この記事は本当に必要なのだろうか。~~

Eclipseでのブランチ操作

＜新規ブランチの作成＞

プロジェクトを右クリック
チーム - 切り替え - 新規ブランチ
ブランチ名を入力後、「完了」

このとき、新規ブランチのチェックアウトをチェックすると、
新規ブランチが作成された後、新規ブランチへ自動的に切り替わります。

＜ブランチのチェックアウト（切り替え）＞

プロジェクトを右クリック
チーム - 切り替え - 「切り替えたいブランチを選択」

この操作で、ブランチを切り替えることができます。

＜ブランチのマージ＞

プロジェクトを右クリック
チーム - マージ
マージしたいブランチを選択後、「マージ」

＜ブランチのリベース＞

プロジェクトを右クリック
チーム - リベース
リベースしたいブランチを選択後、「リベース」

以上です。
さすがeclipseさん！簡単ですね！僕にもできそう！！

これで
「大規模の変更の時はバックアップのコピーを取っておかないと……。」
「あとで見るかもしれないからコメントアウトで残しておこう……。」
といったことを積極的に行う必要はありませんね。

gitの考え方についてはこちらが詳しいです。
サルでもわかるgit入門

2012-11-11

Eclipse と git の連携　～さくらVPS～

さくらVPS git eclipse

ecliseとgitの連携2 ～さくらVPS～ - sonoshouのまじめなブログ
新しく書きました。(2014年1月22日更新）
既にリモート上にgitリポジトリが既に存在する場合は、
こちらをご参照ください。

リモート上にgitリポジトリが存在しない場合は、
以下の記事が参考になるかと思います。

いつでもプログラム書きたいですよね。
サーバーにgitを構築しましょう。
ついでにeclipseと連携させましょう。

今回はおすすめのリンク集となりそうです。
私が構築するにあたって、いくつか詰まった点があります。
そこを重点的に説明していくつもりです。

\------筆者の環境------\
・さくらVPS1GBプラン
・Cent OS
・eclipse 4.2
\----------------------\

この記事は下記リンクを参考にしています。
さくらインターネットをgitの共用リポジトリにする方法 - Dive into the Tech World!

サーバーにgitを構築

私は以下のサイトを見て、gitをインストールしました。
さくらのVPSを改めて使いはじめる 10 -Git、Gitolite、GitHub - アカベコマイリ

アカベコマイリさんのサイトには、毎度本当にお世話になっております。

EclipseにEGitを導入

EGitはGitをEcliseで扱うためのプラグインです。
インストールにあたって、特に難しい点はありません。

Eclipseを起動
ヘルプ - 新規ソフトウェアのインストール
「追加」
名前に「Juno」、ロケーションに「http://download.eclipse.org/releases/juno」を入力
「コラボレーション」から「Eclipse EGit」をチェック
「次へ」

あとは流れで。

EclipseのSSH設定

Eclipseを起動
ウィンドウ - 設定
一般 - ネットワーク接続 - SSH2

ここで、SSH鍵の設定を行う。
(Macの場合、Eclipse - 環境設定)

gitのプロジェクトを作成

Eclipseで開発しているプロジェクトをGitで管理するやり方です。

サーバー上にgitリポジトリを作成

サーバーにログインし、gitのrepositoriesフォルダ内（プロジェクトを作成する場所）で
「git init --bare --shared=true」を実行。

[git@localhost repositories]$ mkdir TestProject.git
[git@localhost repositories]$ cd TestProject.git/
[git@localhost TestProject.git]$ git init --bare --shared=true

以上です。

gitレポジトリの作成は、git専用に作ったユーザーで行って下さい。
他のアカウントでログインしてgitレポジトリを作成してしまうと、
フォルダとファイルの所有者が他のアカウントとなってしまいます。
他のアカウントで行った場合、クライアントとサーバーで同期を行う際、私の環境では、
「error: insufficient permission for adding an object to repository database .git/objects」
というエラーが出てしまいました。

解決するためには、
chownコマンドで所有者を変更して下さい。
例：[chown -R owner:group filename]
参考：error: insufficient permission for adding an object to repository database .git/objects - 604 Error Code Not Found

gitアクセス権限の編集

サーバー上で「/home/user-name/.gitolite/conf/gitolite.conf-compiled.pm」を開く。
以下のように編集して保存。

%repos = (
  'project-name' => {
    'user-name' => [
      [
        1,
        'refs/.*',
        'RW+'
      ]
    ],
    'R' => {
      'user-name' => 1
    },
    'W' => {
      'user-name' => 1
    }
  }
);

これをやらないと、私の環境では、
R access for TestProject DENIED to ユーザ名
というエラーが出ました。

'user-name'とは、
「/home/user-name/.gitolite/keydir」内のパブリックキーのファイル名でした。
（理解が追いついていないのですが、私の場合はそのようでした。）

ローカルgitリポジトリの作成

Eclipseのプロジェクト・エクスプローラーから関連付けるEclipseプロジェクトを右クリック
チーム - プロジェクトの共用
Gitを選択して、「次へ」
リポジトリーの「作成」を押す。
名前にプロジェクト名を入力し、「完了」
「完了」

ローカルgitリポジトリとサーバーのgitリポジトリとの関連付け

ここでは、「msysGit」および「Git for Windows」を使います。

「msysGit」および「Git for Windows」でローカルgitリポジトリ（~/git/)に移動。
「git remote add 」で関連付け。

参考までに以下が私の場合です。

hoge@HOGE ~
$ cd ~/git/TestProject/

hoge@HOGE ~/git/TestProject (master)
$ git remote add origin git.sonoshou.jp:TestProject

EGitの操作

＜コミット＞

プロジェクトを右クリック
チーム - コミット
コミット・メッセージを入力し、（基本的に）ファイル全てにチェック
「コミット」

＜プル＞

プロジェクトを右クリック
チーム - プル

＜初回のプッシュ＞

プロジェクトを右クリック
チーム - リモート - プッシュ
ホストに「ホストネーム」、リポジトリー・パスに「リポジトリー・パス」を入力して、「次へ」
ソース参照(master)と宛先参照(master)を選択して、「Add Spec」
「完了」

＜クローン（リモートとの関連付け）＞

ファイル - インポート
Git - Gitからプロジェクト
ホストに「ホストネーム」、リポジトリー・パスに「リポジトリー・パス」を入力して、「次へ」
masterが選択されていることを確認し、「次へ」
ローカル保管場所を確認して、「次へ」
一般的なプロジェクトのインポートで、「次へ」
「完了」

「ホストネーム」と「リポジトリー・パス」の設定がうまく伝えられなかったので、
画像を添付しておきます。

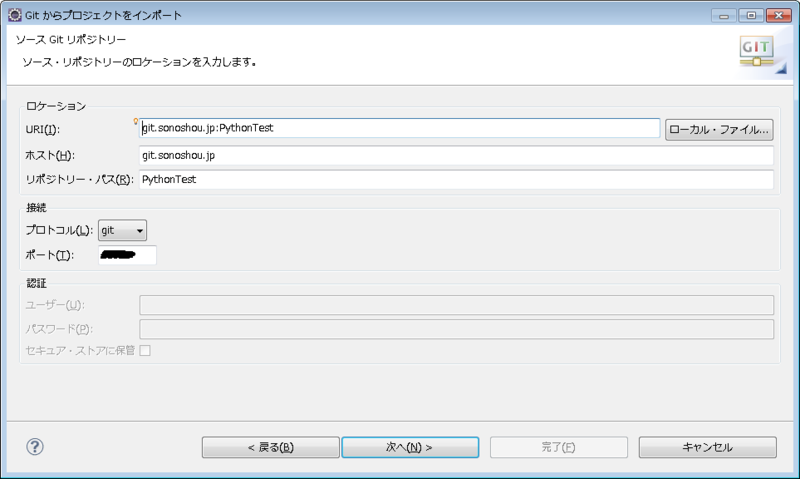
※ただし、私の場合です。
　ホストは「user-name/.ssh/config」内でホストを設定しています。

注意点

eclipseの設定によっては、
pull時に、
「現在のブランチはプル用に構成されていません構成にキー branch.master.merge の値がありません」
と表示される場合があります。

この場合は、Eclipseから、

ウィンドウ - 設定
チーム - Git
「ユーザー設定」タブから「エントリーの追加」
キーに「branch.master.merge」、値に「refs/heads/master」と入力し、「OK」

これで、eclipseからもpullできるようになります。

2012-10-13

python復習まとめ6

python プログラミング

関数の引数をリストで渡す

関数の引数をリストで渡すことができます。便利！

def func(a, b, c):
	print a, b, c

if __name__ == '__main__':
	f = func
	arglist = [1,2,3]
	f(*arglist)

関数のネスト

pythonは関数のネストに対応している。
すなわち、関数の中に関数を定義することができる。
ただし、内側の関数は外側の関数の変数を参照することはできるが、
代入することはできない。

参照元＆より詳しくはこちらへ
Python でネストした関数の定義と、呼び出し

2012-10-11

非負値行列因子分解

機械学習プログラミング python 集合知プログラミング

このエントリーは、集合知プログラミング第８章を参照にしています。

非負値行列因子分解は、データマイニングの手法の一つである。
データの重要な特徴を抽出するために用いられる。
非負値行列因子分解は、non-negative matrix factorizationの日本語訳であり、
よくNMFと省略されるので、こちらの省略形も覚えておきたい。

非負値行列因子分解の基本的なアイディア

非負値行列因子分解は、その名の通り、行列を正の数（非負値）で因子分解することで、
特徴の抽出を行う。
因子分解とは、掛け合わせることで再び分解前の行列を構築できるような
２つの小さな行列を探し出すということである。

非負値行列因子分解の例

以下、具体例を交えながら解説する。

文書の記事と記事内に存在する単語との対応付けがあるとき、
これらに対してNMFで特徴を抽出する。

対応付けの表は以下のようになっているとする。

	apple	lemon	google	tv	gree	book	doraemon
computer of history	5	0	6	2	2	9	0
a lot of fruits	7	5	0	1	0	6	0
dessert in japan	4	3	0	0	0	5	0
new machine	1	0	1	8	1	8	1
what is a smartphone	2	0	4	3	6	6	0

行に記事の名前（カテゴリ名ではない）、列に単語のカウントがあったとする。
例えば、「a lot of fruits」という記事には、
「lemon」という単語が5回出てきたことを意味する。

早速これを非負値行列因子分解にかけてみる。
使用したプログラムは以下である。

# -*- coding: utf-8 -*-
from numpy import *

def difcost(a, b):
	dif = 0
	# 行列の全ての行と列をループする。
	for i in range(shape(a)[0]):
		for j in range(shape(a)[1]):
			# 差を足し合わせる
			dif += pow(a[i,j]-b[i,j],2)
	return dif

def factorize(v, pc=10, iter=50):
	ic=shape(v)[0]	# shape関数は行列の行と列の数を返す。
	fc=shape(v)[1]

	# 重みと特徴の行列をランダムな値で初期化
	w = matrix([[random.random() for j in range(pc)] for i in range(ic)])
	h = matrix([[random.random() for i in range(fc)] for i in range(pc)])

	# 最大でiterの回数だけ操作を繰り返す:
	for i in range(iter):
		wh = w * h

		# 現在の差を計算
		cost = difcost(v, wh)

		# 行列が完全に因子分解されたら終了
		if cost == 0:
			break

		# 特徴の行列を更新
		hn = (transpose(w) * v)
		hd = (transpose(w) * w * h)
		
		h = matrix(array(h)*array(hn)/array(hd))

		# 重みの行列を更新
		wn = (v * transpose(h))
		wd = (w * h * transpose(h))

		w = matrix(array(w)*array(wn)/array(wd))
	
	return w,h

if __name__ == '__main__':
	mat=matrix([[5,0,6,2,2,9,0],
				[7,5,0,1,0,6,0],
				[4,3,0,0,0,5,0],
				[1,0,1,8,1,8,1],
				[2,0,4,3,6,6,0]])

	w,h= factorize(mat,pc=4,iter=100)

	# 分解された行列を出力
	print 'w='
	for i in range(shape(w)[0]):
		for j in range(shape(w)[1]):
			print ('%3f' % w[i,j]),
		print
	print
	print 'h='
	for i in range(shape(h)[0]):
		for j in range(shape(h)[1]):
			print ('%3f' % h[i,j]),
		print
	print
	# 元々の行列を出力
	print 'answer='
	print mat
	print
	# 分解された行列２つを掛け合わせた答えを出力
	print 'w*h='
	wh = w * h
	for i in range(shape(wh)[0]):
		for j in range(shape(wh)[1]):
			print ('%3f' % wh[i,j]),
		print

非負値行列因子分解の初期値はランダムのため、
毎回分解される行列が異なる。
今回は一つの出力結果を例としてあげて考察する。
尚、今回は特徴を4つと定義した。
これを変更するためには、main内のw,h= factorize(mat,pc=4,iter=100)のpc=4を
変更すれば良い。

w=
0.115763 1.394507 1.002702 0.002616
0.101676 0.608862 0.000098 1.524762
0.056321 0.589217 0.003223 0.837026
1.748477 0.097005 0.302305 0.008632
0.192223 0.000058 1.808071 0.001300

h=
0.211139 0.000000 0.001217 4.357839 0.075848 3.833696 0.560386
2.861827 0.110886 1.678718 0.044343 0.000000 4.220322 0.000000
1.058467 0.000000 2.590953 1.249636 2.991750 2.879790 0.000000
3.220199 3.315222 0.000000 0.199414 0.000000 2.062877 0.000000

answer=
[[5 0 6 2 2 9 0]
 [7 5 0 1 0 6 0]
 [4 3 0 0 0 5 0]
 [1 0 1 8 1 8 1]
 [2 0 4 3 6 6 0]]

w*h=
5.085030 0.163304 4.939077 1.819846 3.008614 9.222034 0.064872
6.674068 5.122439 1.022486 0.774269 0.008006 6.105072 0.056978
4.396929 2.840262 0.997549 0.442506 0.013915 4.438564 0.031561
0.994560 0.039372 0.948232 8.003378 1.037040 8.000905 0.979823
1.958723 0.004318 4.684958 3.097369 5.423875 5.946716 0.107719

wの行列は、
行に記事名、列に特徴の値として定義される。
hの行列は、
行に特徴、列に単語名として定義される。

answerは元々の行列であるが、
これがwの行列とhの行列に分解され、
さらにこれらの行列を掛け合わせると、
ほとんどanswer（元の行列）と近くなっていることが確認できる。

さて、この表の見方には少しコツがいる。

まずはwの行列について説明する。
(1,4)の要素（左から１番目、上から４番目）を見てみると、
同列内の他の要素と比べて、1.748477と大きい。
この行は「new machine」なので、
「特徴1」は「new machine」の特徴をよく表していると言える。

また、wの行列について、
(4,2)と(4,3)の要素を見てみると、
こちらも同列内の他の要素と比べると、やや大きい。
この行である「a lot of fruits」と「dessert in japan」は
「特徴4」によく表れているといえ、またこれらの記事は
カテゴリとして近いことが言える。

次に、hの行列について説明する。
(2,4)の要素を見てみると、
同列内の他の要素と比べて、3.315222とかなり大きい。
この列は「lemon」なので、
「特徴4」は「lemon」という単語の重みが大きいことを示している。

以上のことから、「特徴4」は果物系やデザート系をまとめたカテゴリであり、
「lemon」という単語がキーワードとなっていることがわかる。

また、hの行列の7行目はどれも値が変わらない。
７列目は「doraemon」であるが、
この単語は特徴としてはあまり意味をなしていないことがわかる。

このような予想を繰り返すと、
何となくではあるが、このように特徴を捉えると、
うまくwとhの行列を説明できるように思える。

特徴１：機械
特徴２：アップル
特徴３：スマートフォン
特徴４：果物、デザート系

このように行列を分解することによって、
様々な特徴を捉えられることがわかった。

2012-10-11

減衰関数

機械学習プログラミング python 集合知プログラミング

機会学習（データマイニング）をしていると、
各要素の距離に応じた重み付けを行うことがある。
今回は、この時に使われる減衰関数に焦点当てる。

このエントリーは、集合知プログラミング第８章を参照しています。

反比例関数
減法（引算）関数
ガウス関数

これらの関数について説明する。
私の（下手くそな）図を参考にして欲しい。

反比例関数

反比例関数は高速であり、実装も簡単である。
また良い結果が得られるように、分子の値を変更して、調整することができる。
関数の特徴として、距離の近い要素の重みは非常に大きく、
距離が増すと急激に小さくなる。
この特徴は、望ましい場合もあるが、データのノイズに対して非常に敏感になってしまう。

減法（引算）関数

減法関数は定数から距離を引くという非常に単純な関数である。
減法関数は反比例関数と比較して、距離の近いアイテムに重みを与えすぎてしまうという
問題に対応している。
しかし、重みの落ち着く先が0であるために、距離が十分近いと見なされる要素しか
存在しなくなるという問題がある。

ガウス関数

ガウス関数は、反比例関数、減法関数と比較して複雑ではあるが、
これまで２つの問題点を見事に解消している。
ガウス関数の重みは距離が0のときに1となり、距離が増すに従って減少する。
しかし、減法関数とは異なり、完全に0とはならない。
非常に有用ではあるが、これまでの関数よりコードが複雑であり、
関数の評価もあまり速くないということには留意してほしい。

2012-09-29

文章のカテゴリ分け

機械学習プログラミング python 集合知プログラミング

集合知プログラミング第６章を参考にしています。
集合知プログラミングのソースコードはこちらで公開されています。
http://examples.oreilly.com/9780596529321/

本エントリーでは、文章の内容に応じて文章をカテゴライズ（分類する）方法についてです。
自動タグ付けやスパムメールの分類などで用いられます。

単語／カテゴリのカウント

＜サンプル文章＞
('This is a pen', 'good')
('That pen is very good', 'good')
('This pen is so short', 'bad')
('This pencil is mine', 'bad')

＜'pen'が'good'の文章に出てきた回数＞
('pen', 'good') => 2.0
＜'pen'が'bad'の文章に出てきた回数＞
('pen', 'bad') => 1.0

＜'pen'が文章に出てきた回数＞
=> 3.0

＜'good'文章の個数＞
('good') => 2.0
＜'bad'文章の個数＞
('bad') => 2.0

＜全ての文章の数＞
=> 5.0

＜カテゴリのリスト＞
('bad', 'good')

単語／カテゴリの確率

＜'good'文章だったとき'pen'が出現する確率＞＝
＜'pen'が'good'と文章に出てきた回数＞／＜'pen'が文章に出てきた回数＞
したがって、
0.666666666667 = 2.0 / 3.0

推測を始める

以上のやり方は、サンプル文章に対する正しい確率を算出する。
しかし、トレーニングの初期の間や、まれにしか出現しない単語については注意を要する。
例えば、'pencil'という単語は、サンプル文章中に１回しか存在しない。
にもかかわらず、'pencil'という単語が出現したら、現時点では100%で
'bad'であると判断されてしまう。
しかし、今回はサンプル文章が少ないため、たまたま'pencil'は'bad'であると
判断されただけであるにもかかわらず、100%の確率で'bad'であると
判断するのは極端すぎる。
これよりも、単語が他のカテゴリの文章で見つかるに連れて、
値をだんだんと0に近づけるやり方の方が現実的である。

そこで、単語に関する情報が無い場合は仮の確率を決めておくことで、
これらの問題を解決することができる。

ここでは、事前確率を0.5(50%)として推測を行うこととする。
すなわち、'pencil'がどの文章にも出ていない場合は、
'pencil'が'bad'である確率は50%であり、
'pencil'が'bad'であると1回判断された場合は、
'pencil'が'bad'である確率は75%である。

これは次のような計算式から算出される。
(重み * 仮確率 + 出現回数 * 実確率) / (重み + 出現回数)
= (1 * 0.5 + 1 * 1.0) / (1.0 + 1.0)
= 0.75

加重平均（重みがある平均）は、WIkipediaの平均が詳しいので、参照して欲しい。
Wikipedia:平均

また、'good'文章だったとき'pen'が出現する確率は、
確率の表記では、 Pr('pen'|'good') と表記される。

単純ベイズ分類器

以上までで、ある文章中のそれぞれの単語('pen','pencil'など)が
それぞれのカテゴリ('good', 'bad'など)に属する確率を求めた。
次は、丸ごと一つの文章が与えられたときに、カテゴリの属する確率を
求める必要がある。

ドキュメント

例えば、'apple'という単語が20%で'good'にカテゴライズされ、
'banana'という単語が80%で'good'にカテゴライズされるとする。
その場合、'apple'と'banana'の両方の単語が'good'の文章に出現する確率は、
0.2 * 0.8 = 0.16
と計算される。
確率の表記では、 Pr('apple' & 'banana' | 'good') として表記される。

これにより、 Pr(文章|カテゴリ)を計算することができる。
しかし、これはあまり役に立たない。
私たちが知りたいのは、
カテゴリが与えられたとき、任意の文章である確率ではなく、
文章が任意のカテゴリに属する確率を求めることである。
すなわち、 Pr(カテゴリ|文章)を求める必要がある。

ベイズの定理

ベイズの定理は条件付き確率を逆にする方法である。
Pr(A|B) = Pr(B|A) * Pr(A) / Pr(B)
と表記される。
Wikipediaが詳しいので、参考にして欲しい。
Wikipedia:ベイズの定理

ここで、現在の文章とカテゴリの問題に当てはめると、
Pr(文章|カテゴリ)は既に上で求めた。
Pr(カテゴリ)は、文章がこのカテゴリの属する確率なので、
そのカテゴリ中に含まれている文章の数を文章の総数で割れば良い。
すなわち、 Pr(カテゴリ) = カテゴリ中に含まれている文章／文章の総数
pr(文章)は、全ての文章からその文章が選ばれる確率である。
繰り返しになるが、私たちが求めたいのは Pr(カテゴリ|文章) である。
すなわち、 Pr('good'|文章)やPr('bad'|文章)を求めたいわけだが、
文章自体は変わらないので、両者を求める際、Pr(文章)の確率は変わらない。
従って、Pr(文章)はPr(カテゴリ|文章)の大小には影響しないので無視できる。

つまり、
Pr(カテゴリ|文章) = Pr(文章|カテゴリ) * Pr(カテゴリ)
となる。

この計算を各カテゴリに行い、
最も大きい数値を出したカテゴリが属すべきカテゴリである。

すなわち、
属すべきカテゴリ = argmax Pr(文章|カテゴリ) * Pr(カテゴリ)
とも書けるでしょう。

フィッシャー法

フィッシャー法は単純ベイズよりも複雑であるが、
精度が高い場合が多いので、よく用いられる。
フィッシャー法では、文章中のそれぞれの特徴のあるカテゴリでの確率を算出し、
それらをまとめた確率の集合がランダムな集合と比較して高いか低いかをテスト
してカテゴリを決定する。
つまり、　
Pr(カテゴリ|特徴) =
(その特徴を持つ文章がこのカテゴリ中に存在する数) ／ (その特徴を持つ文章の総数)
尚、この方法がうまくいく場合は、それぞれのカテゴリ中の文章の数が
将来的には同数になる場合である。

ただ、フィッシャー法は、
数学的に理解できなかったので、この辺で終了。無念...

2012-09-27

最適化アルゴリズム

機械学習プログラミング python 集合知プログラミング

集合知プログラミングの第５章最適化の一部を自分なりにまとめます。

ヒルクライム法（傾斜上り法）

ヒルクライム法は、ある地点から少し値を変更し、
変更後の値が変更前の値より低ければ採用する。
これを繰り返して行けば、最小値へ近づくことが出来る。

ヒルクライム法には致命的な弱点がある。
例えば、下図のようなグラフを考える。

このように、局所的最小解があるようなグラフでは、
大局的最小解を発見することはできない。

ヒルクライム法は非常に単純な方法で一般的に使われることは無いが、
この後の手法の比較のために説明する。

アルゴリズム

＜初期化処理＞

ランダムな値で変数を初期化。カウントを初期化。

＜反復処理＞

変更する変数を一つ選ぶ。
変数の値を増加させるか、減少させるかを決定する。
変数の値を変更後、新たな変数でコストを算出する。
変更前と変更後のコストの大小を比較する。
変更後のコストが小さければ採用する。
カウンタを進める。

＜終了条件＞

反復回数。

具体例

$3x^4 - 5x^3 + 2x^2$
の最小値を求めてみる。
グラフは既に掲載済みである。

このグラフの特徴として、
0.864付近に大局的最小解があるが、
0付近に局所的最小解がある。

作成したプログラムは以下。

# -+- coding: utf-8 -*-
import random	#ランダムモジュール
import math

def hillclimboptimize(maxcount=5000, cool=0.95, step=0.001):
	# ランダムな値で初期化
	vec = random.randint(-2,2)
	print "start =",vec
	count = 0

	while count < maxcount:
		# 変更する変数を一つ選ぶ。
		# 今回の場合は1次元なので選ぶ必要がない。
		# i = random.randint(0, dimmension-1)
	
		# 変数の値を増加させるか、減少させるかを決定する。
		dir = random.randint(0,1)
		if dir == 0: dir = -step
		else: dir = step

		# 変数の値を変更する。
		newvec = vec + dir

		# 変更前と変更後のコストを計算する。
		newcost = costf(newvec)
		cost = costf(vec)

		# 変更後のコストが小さければ採用する。
		if(newcost < cost):
			vec = newvec
			
		# カウンタを進める。
		count += 1

	return vec
	
def costf(x):
	return (3*(x**4)) - (5*(x**3)) + (2*(x**2))

if __name__ == '__main__':
	print hillclimboptimize()

何回か動かした結果です。

% python hillclimb.py                                      27 木 15:06:34 
start = -2
-1.09252884517e-13||<

% python hillclimb.py                                      27 木 15:08:06 
start = -1
8.81239525796e-16

% python hillclimb.py                                      27 木 15:06:00 
start = 0
0

% python hillclimb.py                                      27 木 15:06:01 
start = 1
0.864

% python hillclimb.py                                      27 木 15:07:25 
start = 2
0.864

このプログラムの初期値は、
-2,-1,0,1,2のいずれかに設定されていますが、
グラフを見て解る通り、
-2,-1,0では0付近に収束し、
1,2では0.864付近に収束していることがわかる。

これらのことから、局所的最小解に収束する可能性が高いという
ヒルクライム法の問題点がわかったのではないでしょうか。

焼きなまし法（アニーリング法）

焼きなまし法は、大域的最適化問題を解く
ヒューリスティックな汎用的アルゴリズムの一つである。
焼きなまし法という名前は、物理現象の焼きなましからヒントを得て、
作成されたことに起因する。

焼きなまし法では温度を表す変数を使う。
この変数は当初は非常に高い値を設定し、アルゴリズムが進むに連れて、
次第に低くなっていくように変化させていく。

各反復では解の中の数字をランダムに選び、いずれかの方向にずらす。
そして、変更前と変更後でコストを計算し、両者を比較する。

もし、新しいコストの方が小さければ、新しい解が現在解となる。
しかし、コストが大きくなるときも、一定の確率で新しい解が現在解となる。
これにより、局所最小解を回避可能な点が焼きなまし法の大きな特徴である。
この一定の確率を決定するのが、初めに説明した温度の変数に当たる。
すなわち、初めは温度が高いため、変更前後でコストが大きくなろうとも、
新しい解として採用されやすくなるが、
アルゴリズムが進むに連れて、だんだんと温度が低くなり、
変更前後でコストが大きくなると、新しい解として採用されにくくなる。

アルゴリズム

＜初期化処理＞

ランダムな値で変数を初期化。

＜反復処理＞

変更する変数を一つ選ぶ。
変数の値を増加させるか、減少させるかを決定する。
変数の値を変更後、新たら変数でコストを算出する。
変更前と変更後のコストの大小を比較する。
変更後のコストが小さければ採用する。コストが大きければ、確率的に採用する。
温度を下げる。

＜終了条件＞

反復回数または温度指定。

具体例

$3x^4 - 5x^3 + 2x^2$
の最小値を求めてみる。
ヒルクライム法の時と同様の問題を解いてみる。

作成したプログラムは以下。

# -+- coding: utf-8 -*-
import random	#ランダムモジュール
import math

def annealingoptimize(T=10000, cool=0.99, step=1):
	# ランダムな値で初期化
	vec = random.randint(-2,2)

	while T > 0.0001:
		# 変更する変数を一つ選ぶ。
		# 今回の場合は1次元なので選ぶ必要がない。
		# i = random.randint(0, dimmension-1)
	
		# 変数の値を増加させるか、減少させるかを決定する。
		dir = random.random()
		dir = (dir - 0.5) * step

		# 変数の値を変更する。
		newvec = vec + dir

		# 変更前と変更後のコストを計算する。
		newcost = costf(newvec)
		cost = costf(vec)

		# 温度から確率を定義する。
		p = pow(math.e, -abs(newcost - cost) / T)
		print p

		# 変更後のコストが小さければ採用する。
		# コストが大きい場合は確率的に採用する。
		if(newcost < cost or random.random() < p):
			vec = newvec
			
		# 温度を下げる
		T = T * cool

	return vec
	
def costf(x):
	return (3*(x**4)) - (5*(x**3)) + (2*(x**2))

if __name__ == '__main__':
	print annealingoptimize()

以上がメインの焼きなまし法による解法です。
実際に正しいのかどうかのテストコードを作成しました。

if __name__ == '__main__':
	success, failure = 0,0
	for i in range(0, 1000):
		ans = annealingoptimize()
		if (ans >= -0.05 and ans <= 0.05):
			failure += 1
		if (ans > 0.8 and ans <= 0.9):
			success += 1
	
	print success,failure

メインの中身をこのように変えてみましょう。
1,000回試行して、大局的最小解に行き着けたか
あるいは、行き着けなかったかを出力します。

結果は以下の通りです。

% python simulated_annealing_simu.py                       27 木 18:57:48 
924 76

成功した回数が924件
失敗した回数が76件
となりました。

単に結果が良い方だけを選択し続けた場合、
局所的最小解にしか収束しない。
しかし、焼きなまし法では、結果が悪い場合も確率的に採用することによって、
局所的最小解から抜け出すことが出来、大局的最小解に収束する。
その結果、ヒルクライム法よりも良い結果を導くことができる。

遺伝的アルゴリズム

遺伝的アルゴリズムは、生物の進化からヒントを得た
最適化アルゴリズムである。

まず、個体群と呼ばれる無作為解の集団を生成する。
そして、最適化のステップごとに個体群の全メンバーに対して
コストが計算されて、解のリスト内で順位を付ける。

解に順位がついたら、新しい個体群（次の世代）を生成する。
まずは、最良の解をいくつかそのまま新しい個体群に入れる。
これをエリート主義という。
残りは最良の解を改変して作られたまったく新しい解で構成する。

こうした解の改変には２種類ある。

突然変異
交叉または交配

突然変異

突然変異は、優れた解に対してランダムに値を変化させることで、新しい解を生成する。

交叉または交配

交配は、優れた解同士の一部を何らかの方法で組み合わせることで、新しい解を生成する。

アルゴリズム

＜初期化処理＞

ランダムな値で個体群を生成。

＜反復処理＞

個体群のコストを計算する。
個体群のソートを行い、結果が良かったものをエリートとする。
エリートから突然変異や交配を行ったものを作成し、新しい個体群（次の世代）を生

成する。
＜終了条件＞

世代数（反復数）。

具体例

$3x^4 - 5x^3 + 2x^2$
の最小値を求めてみる。
ヒルクライム法の時と同様の問題を解いてみる。

作成したプログラムは以下。

# -+- coding: utf-8 -*-
import random	#ランダムモジュール
import math

def geneticoptimize(popnum = 6,popsize=10, step=1,mutprob=0.2,elite=0.2,maxiter=500):

	# 突然変異の操作
	def mutate(vec):
		i = random.randint(0,popnum-1)
		return vec[0:i] + [random.randint(0,9)] + vec[i+1:]

	# 交叉の操作
	def crossover(r1, r2):
		i = random.randint(1, popsize-2)
		return r1[0:i] + r2[i:]
	
	# 初期化個体群の構築
	pop = []
	for i in range(popsize):
		vec = [random.randint(0,9) for v in range(0,popnum)]
		pop.append(vec)

	# 各世代のエリート数
	topelite = int(elite*popsize)

	# メインループ
	scores = []
	for i in range(maxiter):
		for vec in pop:
			x = convertn(vec)
			scores.append([costf(x),vec])
		scores.sort()
		ranked = [v for (s,v) in scores]

		# 結果が良かったものをエリートとする。
		pop=ranked[0:topelite]

		# エリートから突然変異や交配を行ったものを作成し、
		# 新しい個体群（次の世代）を生成する。
		while len(pop)<popsize:
			if random.random()<mutprob:

				# 突然変異
				c = random.randint(0, topelite)
				pop.append(mutate(ranked[c]))

			else:

				# 交叉
				c1=random.randint(0, topelite)
				c2=random.randint(0, topelite)
				pop.append(crossover(ranked[c1], ranked[c2]))
		
	return convertn(scores[0][1])


def costf(x):
	return (3*(x**4)) - (5*(x**3)) + (2*(x**2))

def convertn(vec):
	x,y = 0,0
	for v in vec:
		x += v * (10 ** y)
		y -= 1
	return x

if __name__ == '__main__':
	
	print geneticoptimize()

以上がメインの焼きなまし法による解法です。
実際に正しいのかどうかのテストコードを作成しました。

if __name__ == '__main__':
	success, failure = 0,0
	for i in range(0, 100):
		ans = annealingoptimize()
		if (ans >= -0.05 and ans <= 0.05):
			failure += 1
		if (ans > 0.8 and ans <= 0.9):
			success += 1
	
	print success,failure

メインの中身をこのように変えてみましょう。
100回試行して、大局的最小解に行き着けたか
あるいは、行き着けなかったかを出力します。

結果は以下の通りです。

% python genetic_simu.py                       27 木 23:37:32 
100 0

成功した回数が100件
失敗した回数が0件
となりました。

焼きなまし法よりも遺伝的アルゴリズムの方が結果が良くなりました。
しかし、今回の成功、失敗の判断は、
-0.05 <= ans <= 0.05 なら失敗
0.8 < ans <= 0.9 なら成功
と大変曖昧なため、一概にも遺伝的アルゴリズムの方が優れているとは言えません。
また、焼きなまし法では1,000回で比較していましたが、
遺伝的アルゴリズムは時間がかかったため、100回で比較しました。

焼きなまし法は最終的にはヒルクライムと同等の動きとなるため、
（大局的な最小解に収束するかどうかはわかりませんが、）
必ず局所的最小解に収束するのに対し、
遺伝的アルゴリズムは確率依存ですので、安定的な性能が出せるかどうかはわかりませ
ん。

ただ、それでも遺伝的アルゴリズムの汎用性の高さ、精度の高さは目を見張るものがあ
ります。